14平均律
14平均律の音程と近似値
各周波数比の大きさが16以内で表現される純正音程は以下のようになる。これはedjirulerを用いて、[number of equal divisions=14, interval of equivalence=2, integer limit=16, threshold of JI pitch inclusion=0.25]というパラメータで生成したものである。
| EDO | interval | cent | DMS | The "neighborhood" of JI | Japanese name | ratio | diff cent | cent | diff DMS | DMS |
| 14 | 0 | 0.00 | 0.00 | |||||||
| 1 | 85.71 | 25.71 | ||||||||
| 2 | 171.43 | 51.43 | 3/4-tone, undecimal neutral second | 3/4全音、11リミットの中立的な2度 | 12/11 | 20.79 | 150.64 | 6.24 | 45.19 | |
| 2 | 171.43 | 51.43 | 4/5-tone, Ptolemy's second | 4/5全音、プトレマイオスの2度 | 11/10 | 6.42 | 165.00 | 1.93 | 49.50 | |
| 2 | 171.43 | 51.43 | minor whole tone | 小全音 | 10/9 | -10.98 | 182.40 | -3.29 | 54.72 | |
| 3 | 257.14 | 77.14 | tridecimal 5/4-tone | 13リミットの5/4全音 | 15/13 | 9.40 | 247.74 | 2.82 | 74.32 | |
| 3 | 257.14 | 77.14 | septimal minor third | 7リミットの短3度 | 7/6 | -9.73 | 266.87 | -2.92 | 80.06 | |
| 4 | 342.86 | 102.86 | undecimal neutral third | 11リミットの中立3度 | 11/9 | -4.55 | 347.41 | -1.37 | 104.22 | |
| 4 | 342.86 | 102.86 | tridecimal neutral third | 13リミットの中立3度 | 16/13 | -16.62 | 359.47 | -4.98 | 107.84 | |
| 5 | 428.57 | 128.57 | undecimal diminished fourth or major third | 11リミットの減4度または長3度 | 14/11 | 11.06 | 417.51 | 3.32 | 125.25 | |
| 5 | 428.57 | 128.57 | septimal major third, BP third | 7リミットの長3度、ボーレン・ピアスの3度 | 9/7 | -6.51 | 435.08 | -1.95 | 130.53 | |
| 6 | 514.29 | 154.29 | perfect fourth | 完全4度 | 4/3 | 16.24 | 498.04 | 4.87 | 149.41 | |
| 7 | 600.00 | 180.00 | septimal or Huygens' tritone, BP fourth | 7リミットまたはヒュイゲンの3全音、ボーレン・ピアスの4度 | 7/5 | 17.49 | 582.51 | 5.25 | 174.75 | |
| 7 | 600.00 | 180.00 | Euler's tritone | レオンハルト・オイラーの3全音 | 10/7 | -17.49 | 617.49 | -5.25 | 185.25 | |
| 8 | 685.71 | 205.71 | perfect fifth | 完全5度 | 3/2 | -16.24 | 701.96 | -4.87 | 210.59 | |
| 9 | 771.43 | 231.43 | septimal minor sixth | 7リミットの長6度 | 14/9 | 6.51 | 764.92 | 1.95 | 229.47 | |
| 9 | 771.43 | 231.43 | undecimal augmented fifth | 11リミットの増5度 | 11/7 | -11.06 | 782.49 | -3.32 | 234.75 | |
| 10 | 857.14 | 257.14 | tridecimal neutral sixth | 13リミットの中立6度 | 13/8 | 16.62 | 840.53 | 4.98 | 252.16 | |
| 11 | 942.86 | 282.86 | septimal major sixth | 7リミットの長6度 | 12/7 | 9.73 | 933.13 | 2.92 | 279.94 | |
| 12 | 1028.57 | 308.57 | just minor seventh, BP seventh | 純正短7度、ボーレン・ピアスの7度 | 9/5 | 10.98 | 1017.60 | 3.29 | 305.28 | |
| 12 | 1028.57 | 308.57 | 21/4-tone, undecimal neutral seventh | 21/4全音、11リミットの中立7度 | 11/6 | -20.79 | 1049.36 | -6.24 | 314.81 | |
| 13 | 1114.29 | 334.29 | ||||||||
| 14 | 1200.00 | 360.00 |
ランク2テンペラメント
ハーモニー
14平均律の特徴は、5:7:9:11:17:19を除いて低いリミットのJIアプローチを探すことには向いていないということである。しかしながら、7/5、7/6、9/7、10/7、10/9、11/7、11/9、そして11/10は近似であると認識することができる。もし14平均律がこれらの近似であると認識できるのであれば、高い損傷を負い本ページ最後のコンマのリストをテンパーアウトする11リミットテンペラメントは、複雑ではなく、シンプルなテンペラメントであるという結論になるだろう。
14平均律は非常にわずかなゼンハーモニックアピールを持ち、これは17平均律に似ている。これは12TETでは通常2つであるのに対し、3つのタイプの3度と3つのタイプの6度を持つためである。14平均律はまた4度と5度と認識できるものも持つため、これは音を足すのではない、3和音の響きの代わりの探求によい。5L4sのトライアド・リッチ9音MOS音階をもち、そこで9音のうち7音がサブマイナー、スーパーメジャー、中立3和音のためのトニックをもつ。
記譜法
Ivor Darregがこの記事を書いた。
14音階は、7音平均律の音に加え、通常のシャープとフラットを使うという新しい状況を提供する。このことは7音の5度圏(明らかに歪んでいるが)がすでにF C G D A E Bというように記譜され名づけられているため、混同してしまうようなミスリードを引き起こしそうである。しかし14音の5度圏は存在しない。そこには単純に、7つの5度が円の中に交わることなく2セット存在する。したがってBb、B、またはBナチュラルとFシャープのようなものは、14音システム音程の中では5度では「ない」のだろう。B Fのような音も、7や14の中ではCGやAEが引き起こすようなとても歪んだ5度の響きがする。私たちが提案するのは新しい14音の呼び方であり、F* C* G* D* A* E* B*という7つのセットを2つ目とすることである。アスタリスクは5線譜に書きたいと思うような、望むものでよく、矢印などでもよい。
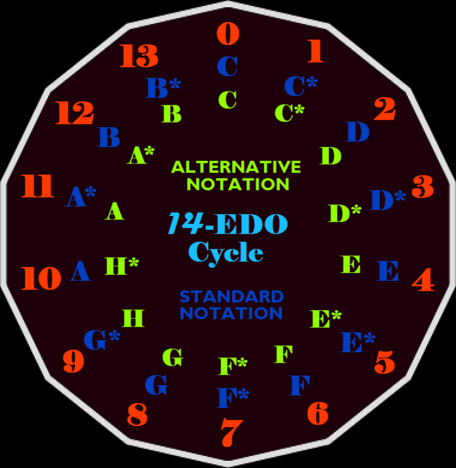
下の図はTDWによって作成されたものであり、提案されたものと同じ推薦される「スタンダード・ノーテーション」である。
|
| Intervallic Cycle of 14 steps Equal per Octave |
イメージ
コンマをなだらかにする
14平均律を< 14 22 33 39 48 52 |ヴァルとみなした時、次のリストのコンマをテンパーアウトする。
| Comma | Monzo | Value (Cents) | Name 1 | Name 2 |
|---|---|---|---|---|
| 2187/2048 | | -11 7 > | 113.69 | Apotome | |
| 2048/2025 | | 11 -4 -2 > | 19.55 | Diaschisma | |
| 36/35 | | 2 2 -1 -1 > | 48.77 | Septimal Quarter Tone | |
| 49/48 | | -4 -1 0 2 > | 35.70 | Slendro Diesis | |
| 1728/1715 | | 6 3 -1 -3 > | 13.07 | Orwellisma | Orwell Comma |
| 10976/10935 | | 5 -7 -1 3 > | 6.48 | Hemimage | |
| | 47 -7 -7 -7 > | 0.34 | Akjaysma | 5\7 Octave Comma | |
| 99/98 | | -1 2 0 -2 1 > | 17.58 | Mothwellsma | |
| 243/242 | | -1 5 0 0 -2 > | 7.14 | Rastma | |
| 385/384 | | -7 -1 1 1 1 > | 4.50 | Keenanisma | |
| 91/90 | | -1 -2 -1 1 0 1 > | 19.13 | Superleap | |
| 676/675 | | 2 -3 -2 0 0 2 > | 2.56 | Parizeksma |
モード
2 2 2 2 2 2 2 = 7edo
2 1 2 1 2 1 2 1 2 - MOS of 5L4s
2 1 2 1 2 1 2 2 1 - MOS of 5L4s
2 1 2 1 2 2 1 2 1 - MOS of 5L4s
2 1 1 2 1 2 1 1 2 1 - MOS of 4L6s
2 1 1 1 2 1 1 2 1 1 1 - MOS of 3L8s
1 1 2 1 1 1 2 1 1 1 2 - MOS of 3L8s
本
Sword, Ron. "Tetradecaphonic Scales for Guitar" IAAA Press. First Ed: June 2009.

