13平均律

---

最も2.5.9.11.13.17.19.21に近似する音律

13平均律は周波数比2のオクターブを13個の均等なパートに分割するシステムを参照する。それは6番目の素数平均律であり、11平均律の後であり17平均律の前の平均律である。600セントより小さいステップ（6ステップ、553.84セント）は、最も近い12平均律の近似よりも狭い。そして600セントより大きいもの（7ステップ、646.15セント）は幅広い。これは巧妙な耳のトリックを起こす。12平均律から連想されるメロディーは、慣れていない場所へ素早くたどり着く。

21アドリミットJIのテンペラメントとしてみなすと、13平均律は素晴らしい11番目と21番目の倍音に近似する。そして5、9、13、17、19倍音にもそれなりに近づくことができる。一番の目的は、3、7、15倍音の近似と認識するものを与えないことである。3倍音の響きとそれなりに近い響きが発生しないということは、13平均律が慣習的な音楽に適していないということを示す。しかし11、13、21の周波数とはとても良い近似値であり、とてもゼンハーモニックチューニングを作り出す。これらの独自性は12平均律の表現から離れはしないけれども。評価は不協和であるものの、それは2.5.9.11.13.17.19.21サブグループであり、素晴らしいランク1のテンペラメントである。そして小さいサイズのための、複雑に一致する多くのレパートリーを持つ。

13平均律の音程と近似値

「The “neighborhood” of JI」の一覧はこちら（huygens-fokker）を参照のこと。各周波数比の大きさが16以内で表現される純正音程は以下のようになる。これはedjirulerを用いて、[number of equal divisions=13, interval of equivalence=2, integer limit=16, threshold of JI pitch inclusion=0.2]というパラメータで生成したものである。

EDO	interval	cent	DMS	The "neighborhood" of JI	Japanese name	ratio	diff cent	cent	diff DMS	DMS
13	0	0.00	0.00
	1	92.31	27.69
	2	184.62	55.38	minor whole tone	小全音	10/9	2.21	182.40	0.66	54.72
	3	276.92	83.08	septimal minor third	7リミットの短3度	7/6	10.05	266.87	3.02	80.06
	3	276.92	83.08	tridecimal minor third	13リミットの短3度	13/11	-12.29	289.21	-3.69	86.76
	4	369.23	110.77	tridecimal neutral third	13リミットの中立3度	16/13	9.76	359.47	2.93	107.84
	4	369.23	110.77	major third	長3度	5/4	-17.08	386.31	-5.12	115.89
	5	461.54	138.46	tridecimal semi-diminished fourth	13リミットの準減4度	13/10	7.32	454.21	2.20	136.26
	6	553.85	166.15	undecimal augmented fourth	11リミットの増4度	15/11	16.90	536.95	5.07	161.09
	6	553.85	166.15	undecimal semi-augmented fourth	11リミットの準増5度	11/8	2.53	551.32	0.76	165.40
	7	646.15	193.85	tridecimal diminished fifth	13リミットの減5度	13/9	9.54	636.62	2.86	190.99
	7	646.15	193.85	undecimal semi-diminished fifth	11リミットの準減5度	16/11	-2.53	648.68	-0.76	194.60
	8	738.46	221.54
	9	830.77	249.23	minor sixth	短6度	8/5	17.08	813.69	5.12	244.11
	9	830.77	249.23	tridecimal neutral sixth	13リミットの中立6度	13/8	-9.76	840.53	-2.93	252.16
	10	923.08	276.92	septimal major sixth	7リミットの長6度	12/7	-10.05	933.13	-3.02	279.94
	11	1015.38	304.62	just minor seventh, BP seventh	純正短7度、ボーレン・ピアスの7度	9/5	-2.21	1017.60	-0.66	305.28
	12	1107.69	332.31
	13	1200.00	360.00

13平均律の音階

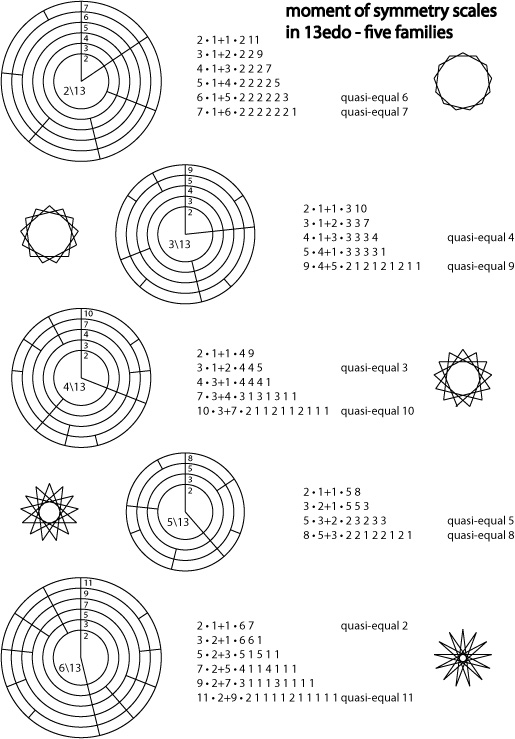
13という素数の特徴によって、13平均律はいくつかのゼンハーモニックMOS音階（moment of symmetry scales）を形作る。下のダイアグラムはMOS音階の5音「ファミリー」を示す。これらは213（13平均律の2音程）、313、413、513、6//13のチェーンによって作成される。

13edo horograms.pdf

Ery Wilsonが先駆者となったホラグラムをもとに、Andrew Heathwaiteが作成したダイアグラム。

13平均律のもう一つのきちんとした様相として、余分な半音を加えるか、現在の半音を全音に変えることで、どんな12平均律の音階も13平均律の音階に「変えられる」ということである。このため、13平均律のメロディーはとても不思議で、類似した方法でフレーズを始めると、即座に予想外の何かに導かれる。

13平均律のハーモニー

一般的な考えとは逆に、13平均律で協和音は可能である。しかし12平均律やピタゴラス、ミーントーンなどをベースとしたチューニングの使い方とは徹底的に異なったアプローチを要求する。一般的な12平均律の長3和音や短3和音の近似値を13平均律の中で試みるとき、ゴールを0-3-7、0-4-7、0-3-8、0-4-8とするなら、13平均律では荒くなるので通常断念せざるを得ない。13平均律で通常最も協和するハーモニーは、「3度の積み重ね」ではない。13平均律の最も強い不協和は、オクターブのミドルトーン、つまり音程が6、7、8ステップに近い時である。代わりに、全音の積み重ね、または全音と短3度のミックスの積み重ねで、しばしば良い結果が生み出される。たとえば、13平均律をハーモニック2.5.9.11.13のテンペラメントサブグループとしてみなす方法である。これは実際見事に演じる。そして4:5:9:11:13に近い0-4-15-19-22のコードはとても人を納得させる。より大きなサブグループは、2*13 subgroup2.9.5.21.11.13である。13は26ETのようなコンマとチューニングをもつ。

この場合、私たちは13平均律の長9度が12平均律の完全5度や他のミーントーン平均律と似ていると想定することができる。これは11/8や5/4などが続く13平均律において、長2度や長9度が2/1に次いで最も協和することを意味する。4:5:9コードはそれゆえ基本的な13平均律のトライアドであると考えることができる。

2.9.5.11.13サブグループは、45/44と65/64,そして81/80コンマを持ち、POTEジェネレーター185.728セントとともにリニアーテンペラメントを導く。それは非常に2//13に近い。これをジェネレーターとして使うと、そして7音（6L1s）の2つの完全なペンタを利用する。同様に2つの4:5:9:11テトラと、1つの4:5:9:13テトラも利用できる。これらのトライアドとテトラは、13平均律の中でおそらくもっとも協和するベースソノリティーであり、長3和音や短3和音と似た手法を演じるという想定ができる。しかしながら、ほかのOrwellコードのようなソノリティーも同時に感じられる。

のアプローチは特定の作曲家と理論家によって探求されており、大まかなものは下に示される。

Play the 4:5:9 chord:

Play the 4:5:9:11 chord:

Play the 4:5:9:13 chord:

Play the 4:5:9:21 chord:

13平均律の記譜法と作曲のアプローチ

13平均律は多くの作曲家や理論家から興味を持たれており、何人かは記譜法と作曲に関するアプローチの提案を行っている。

コンマをなだらかにする

13平均律を<13 21 30 36 45 48|ヴァルとみなした時、次のリストのコンマをテンパーアウトする。

Comma	Monzo	Value (Cents)	Name 1	Name 2	Name 3
2109375/2097152	| -21 3 7 >	10.06	Semicomma	Fokker Comma
1029/1000	| -3 1 -3 3 >	49.49	Keega
525/512	| -9 1 2 1 >	43.41	Avicennma	Avicenna's Enharmonic Diesis
64/63	| 6 -2 0 -1 >	27.26	Septimal Comma	Archytas' Comma	Leipziger Komma
64827/64000	| -9 3 -3 4 >	22.23	Squalentine
3125/3087	| 0 -2 5 -3 >	21.18	Gariboh
3136/3125	| 6 0 -5 2 >	6.08	Hemimean
121/120	| -3 -1 -1 0 2 >	14.37	Biyatisma
441/440	| -3 2 -1 2 -1 >	3.93	Werckisma