72edo

Prime factorization

2³ × 3²

Step size

16.6667¢

Fifth

42\72 (700¢) (→7\12)

Semitones (A1:m2)

6:6 (100¢ : 100¢)

Consistency limit

17

Distinct consistency limit

11

Special properties

zeta peak
zeta integral
zeta gap

English Wikipedia has an article on:

72 equal temperament

72 equal divisions of the octave (abbreviated 72edo or 72ed2), also called 72-tone equal temperament (72tet) or 72 equal temperament (72et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 72 equal parts of about 16.7 ¢ each. Each step represents a frequency ratio of 2^1/72, or the 72nd root of 2.

Each step of 72edo is called a morion (plural moria). This produces a twelfth-tone tuning, with the whole tone measuring 200 cents, the same as in 12edo. 72edo is also a superset of 24edo, a common and standard tuning of Arabic music, and has itself been used to tune Turkish music.

Composers that used 72edo include Ivan Wyschnegradsky, Julián Carrillo (who is better associated with 96edo), Ezra Sims, James Tenney, Georg Friedrich Haas and the jazz musician Joe Maneri.

Theory

72edo approximates 11-limit just intonation exceptionally well, is consistent in the 17-limit, and is the ninth zeta integral tuning. The octave, fifth and fourth are the same size as they would be in 12edo, 72, 42 and 30 steps respectively, but the classic major third (5/4) measures 23 steps, not 24, and other 5-limit major intervals are one step flat of 12edo while minor ones are one step sharp. The septimal minor seventh (7/4) is 58 steps, while the undecimal semiaugmented fourth (11/8) is 33.

72edo is an excellent tuning for the miracle temperament, especially the 11-limit version, and the related rank-3 temperament prodigy, and is a good tuning for other temperaments and scales, including wizard, harry, catakleismic, compton, unidec and tritikleismic.

The 13th harmonic (octave reduced) is so closely mapped on acoustic phi that 72edo could be treated as a 2.3.5.7.11.ϕ.17 temperament.

72edo is the smallest multiple of 12edo that (just barely) has another diatonic fifth, 43\72, an extremely hard diatonic fifth suitable for a 5edo circulating temperament.

Prime harmonics

Approximation of prime harmonics in 72edo
Harmonic		2	3	5	7	11	13	17	19	23	29	31
Error	absolute (¢)	+0.00	-1.96	-2.98	-2.16	-1.32	-7.19	-4.96	+2.49	+5.06	+3.76	+4.96
Error	relative (%)	+0	-12	-18	-13	-8	-43	-30	+15	+30	+23	+30
Steps (reduced)		72 (0)	114 (42)	167 (23)	202 (58)	249 (33)	266 (50)	294 (6)	306 (18)	326 (38)	350 (62)	357 (69)

Subsets and supersets

Since 72 factors into 2³ × 3², 72edo has subset edos 2, 3, 4, 6, 8, 9, 12, 18, 24, and 36. 144edo, which doubles it, provides a possible correction to its approximate harmonic 13.

Intervals

Degrees	Cents	Approximate Ratios *	Ups and Downs Notation			SKULO interval names and notation			(K, S, U)
0	0.000	1/1	P1	perfect unison	D	P1	perfect unison	D	D
1	16.667	81/80	^1	up unison	^D	K1, L1	comma-wide unison, large unison	KD, LD	KD
2	33.333	45/44, 64/63	^^	dup unison	^^D	S1, O1	super unison, on unison	SD, OD	SD
3	50.000	33/32	^³1, v³m2	trup unison, trudminor 2nd	^³D, v³Eb	U1, H1, hm2	uber unison, hyper unison, hypominor 2nd	UD, HD, uEb	UD, uEb
4	66.667	25/24	vvm2	dudminor 2nd	vvEb	kkA1, sm2	classic aug unison, subminor 2nd	kkD#, sEb	sD#, (kkD#), sEb
5	83.333	21/20	vm2	downminor 2nd	vEb	kA1, lm2	comma-narrow aug unison, little minor 2nd	kD#, lEb	kD#, kEb
6	100.000	35/33, 17/16, 18/17	m2	minor 2nd	Eb	m2	minor 2nd	Eb	Eb
7	116.667	15/14, 16/15	^m2	upminor 2nd	^Eb	Km2	classic minor 2nd	KEb	KEb
8	133.333	27/25, 13/12, 14/13	v~2	downmid 2nd	^^Eb	Om2	on minor 2nd	OEb	SEb
9	150.000	12/11	~2	mid 2nd	v³E	N2	neutral 2nd	UEb/uE	UEb/uE
10	166.667	11/10	^~2	upmid 2nd	vvE	oM2	off major 2nd	oE	sE
11	183.333	10/9	vM2	downmajor 2nd	vE	kM2	classic/comma-narrow major 2nd	kE	kE
12	200.000	9/8	M2	major 2nd	E	M2	major 2nd	E	E
13	216.667	25/22, 17/15	^M2	upmajor 2nd	^E	LM2	large major 2nd	LE	KE
14	233.333	8/7	^^M2	dupmajor 2nd	^^E	SM2	supermajor 2nd	SE	SE
15	250.000	81/70, 15/13	^³M2, v³m3	trupmajor 2nd, trudminor 3rd	^³E, v³F	HM2, hm3	hypermajor 2nd, hypominor 3rd	HE, hF	UE, uF
16	266.667	7/6	vvm3	dudminor 3rd	vvF	sm3	subminor 3rd	sF	sF
17	283.333	33/28, 13/11, 20/17	vm3	downminor 3rd	vF	lm3	little minor 3rd	lF	kF
18	300.000	25/21	m3	minor 3rd	F	m3	minor 3rd	F	F
19	316.667	6/5	^m3	upminor 3rd	^F	Km3	classic minor 3rd	KF	KF
20	333.333	40/33, 17/14	v~3	downmid 3rd	^^F	Om3	on minor third	OF	SF
21	350.000	11/9	~3	mid 3rd	^³F	N3	neutral 3rd	UF/uF#	UF/uF#
22	366.667	99/80, 16/13, 21/17	^~3	upmid 3rd	vvF#	oM3	off major 3rd	oF#	sF#
23	383.333	5/4	vM3	downmajor 3rd	vF#	kM3	classic major 3rd	kF#	kF#
24	400.000	44/35	M3	major 3rd	F#	M3	major 3rd	F#	F#
25	416.667	14/11	^M3	upmajor 3rd	^F#	LM3	large major 3rd	LF#	KF#
26	433.333	9/7	^^M3	dupmajor 3rd	^^F#	SM3	supermajor 3rd	SF#	SF#
27	450.000	35/27, 13/10	^³M3, v³4	trupmajor 3rd, trud 4th	^³F#, v³G	HM3, h4	hypermajor 3rd, hypo 4th	HF#, hG	UF#, uG
28	466.667	21/16, 17/13	vv4	dud 4th	vvG	s4	sub 4th	sG	sG
29	483.333	33/25	v4	down 4th	vG	l4	little 4th	lG	kG
30	500.000	4/3	P4	perfect 4th	G	P4	perfect 4th	G	G
31	516.667	27/20	^4	up 4th	^G	K4	comma-wide 4th	KG	KG
32	533.333	15/11	^^4, v~4	dup 4th, downmid 4th	^^G	O4	on 4th	OG	SG
33	550.000	11/8	~4	mid 4th	^³G	U4/N4	uber 4th / neutral 4th	UG	UG
34	566.667	25/18, 18/13	^~4, vvA4	upmid 4th, dudaug 4th	vvG#	kkA4, sd5	classic aug 4th, sub dim 5th	kkG#, sAb	SG#, (kkG#), sAb
35	583.333	7/5	vA4, vd5	downaug 4th, downdim 5th	vG#, vAb	kA4, ld5	comma-narrow aug 4th, little dim 5th	kG#, lAb	kG#, kAb
36	600.000	99/70, 17/12	A4, d5	aug 4th, dim 5th	G#, Ab	A4, d5	aug 4th, dim 5th	G#, Ab	G#, Ab
37	616.667	10/7	^A4, ^d5	upaug 4th, updim 5th	^G#, ^Ab	LA4, Kd5	large aug 4th, comma-wide dim 5th	LG#, KAb	KG#, KAb
38	633.333	36/25, 13/9	v~5, ^^d5	downmid 5th, dupdim 5th	^^Ab	SA4, KKd5	super aug 4th, classic dim 5th	SG#, KKAb	SG#, SAb, (KKAb)
39	650.000	16/11	~5	mid 5th	v³A	u5/N5	unter 5th / neutral 5th	uA	uA
40	666.667	22/15	vv5, ^~5	dud 5th, upmid 5th	vvA	o5	off 5th	oA	sA
41	683.333	40/27	v5	down 5th	vA	k5	comma-narrow 5th	kA	kA
42	700.000	3/2	P5	perfect 5th	A	P5	perfect 5th	A	A
43	716.667	50/33	^5	up 5th	^A	L5	large fifth	LA	KA
44	733.333	32/21	^^5	dup 5th	^^A	S5	super fifth	SA	SA
45	750.000	54/35, 17/11	^³5, v³m6	trup 5th, trudminor 6th	^³A, v³Bb	H5, hm6	hyper fifth, hypominor 6th	HA, hBb	UA, uBb
46	766.667	14/9	vvm6	dudminor 6th	vvBb	sm6	superminor 6th	sBb	sBb
47	783.333	11/7	vm6	downminor 6th	vBb	lm6	little minor 6th	lBb	kBb
48	800.000	35/22	m6	minor 6th	Bb	m6	minor 6th	Bb	Bb
49	816.667	8/5	^m6	upminor 6th	^Bb	Km6	classic minor 6th	kBb	kBb
50	833.333	81/50, 13/8	v~6	downmid 6th	^^Bb	Om6	on minor 6th	oBb	sBb
51	850.000	18/11	~6	mid 6th	v³B	N6	neutral 6th	UBb, uB	UBb, uB
52	866.667	33/20, 28/17	^~6	upmid 6th	vvB	oM6	off major 6th	oB	sB
53	883.333	5/3	vM6	downmajor 6th	vB	kM6	classic major 6th	kB	kB
54	900.000	27/16	M6	major 6th	B	M6	major 6th	B	B
55	916.667	56/33, 17/10	^M6	upmajor 6th	^B	LM6	large major 6th	LB	KB
56	933.333	12/7	^^M6	dupmajor 6th	^^B	SM6	supermajor 6th	SB	SB
57	950.000	121/70	^³M6, v³m7	trupmajor 6th, trudminor 7th	^³B, v³C	HM6, hm7	hypermajor 6th, hypominor 7th	HB, hC	UB, uC
58	966.667	7/4	vvm7	dudminor 7th	vvC	sm7	subminor 7th	sC	sC
59	983.333	44/25	vm7	downminor 7th	vC	lm7	little minor 7th	lC	kC
60	1000.000	16/9	m7	minor 7th	C	m7	minor 7th	C	C
61	1016.667	9/5	^m7	upminor 7th	^C	Km7	classic/comma-wide minor 7th	KC	KC
62	1033.333	20/11	v~7	downmid 7th	^^C	Om7	on minor 7th	OC	SC
63	1050.000	11/6	~7	mid 7th	^³C	N7, hd8	neutral 7th, hypo dim 8ve	UC/uC#, hDb	UC/uC#, uDb
64	1066.667	50/27	^~7	upmid 7th	vvC#	oM7, sd8	off major 7th, sub dim 8ve	oC#, sDb	sC#, sDb
65	1083.333	15/8	vM7	downmajor 7th	vC#	kM7, ld8	classic major 7th, little dim 8ve	kC#, lDb	kC#, kDb
66	1100.000	66/35, 17/9	M7	major 7th	C#	M7, d8	major 7th, dim 8ve	C#, Db	C#, Db
67	1116.667	21/11	^M7	upmajor 7th	^C#	LM7, Kd8	large major 7th, comma-wide dim 8ve	LC#, KDb	KC#, KDb
68	1133.333	27/14, 48/25	^^M7	dupmajor 7th	^^C#	SM7, KKd8	supermajor 7th, classic dim 8ve	SC#, KKDb	SC#, SDb, (KKDb)
69	1150.000	35/18	^³M7, v³8	trupmajor 7th, trud octave	^³C#, v³D	HM7, u8, h8	hypermajor 7th, unter 8ve, hypo 8ve	HC#, uD, hD	UC#, uDb, uD
70	1166.667	49/25	vv8	dud octave	vvD	s8, o8	sub 8ve, off 8ve	sD, oD	sD
71	1183.333	99/50	v8	down octave	vD	k8, l8	comma-narrow 8ve, little 8ve	kD, lD	kD
72	1200.000	2/1	P8	perfect octave	D	P8	perfect octave	D	D

* based on treating 72edo as a 17-limit temperament. For lower limits see Table of 72edo intervals.

Interval quality and chord names in color notation

Combining ups and downs notation with color notation, qualities can be loosely associated with colors:

Quality	Color	Monzo Format	Examples
dudminor	zo	(a b 0 1)	7/6, 7/40
minor	fourthward wa	(a b), b < -1	32/27, 16/9
upminor	gu	(a b -1)	6/5, 9/5
downmid	luyo	(a b 1 0 -1)	15/11
downmid	tho	(a b 0 0 0 1)	13/8, 13/9
mid	ilo	(a, b, 0, 0, 1)	11/9, 11/6
mid	lu	(a, b, 0, 0, -1)	12/11, 18/11
upmid	logu	(a b -1 0 1)	11/10
upmid	thu	(a b 0 0 0 -1)	16/13, 18/13
downmajor	yo	(a b 1)	5/4, 5/3
major	fifthward wa	(a b), b > 1	9/8, 27/16
dupmajor	ru	(a, b, 0, -1)	9/7, 12/7

All 72edo chords can be named using ups and downs. An up, down or mid after the chord root affects the 3rd, 6th, 7th, and/or the 11th (every other note of a stacked-3rds chord 6-1-3-5-7-9-11-13). Alterations are always enclosed in parentheses, additions never are. Here are the zo, gu, ilo, yo and ru triads:

Color of the 3rd	JI Chord	Notes as Edosteps	Notes of C Chord	Written Name	Spoken Name
zo	6:7:9	0-16-42	C vvEb G	Cvvm	C dudminor
gu	10:12:15	0-19-42	C ^Eb G	C^m	C upminor
ilo	18:22:27	0-21-42	C v3E G	C~	C mid
yo	4:5:6	0-23-42	C vE G	Cv	C downmajor or C down
ru	14:18:27	0-26-42	C ^^E G	C^^	C dupmajor or C dup

For a more complete list, see Ups and Downs Notation #Chord names in other EDOs.

Remembering the pitch structure

The pitch structure is very easy to remember. In 72tet, 12edo is the Pythagorian ring; id est, every 6 degrees is the 3-limit.

Then, after each subsequent degree in reverse, a new prime limit is unveiled from it:

-1 degree corrects 5/4 (80/81)
-2 degrees corrects 7/4 (63/64)
+3 degrees corrects 11/8 (33/32)
+2 degrees corrects 13/8 (1053/1024)
0 degree corrects 17/16 and 19/16 (4131/4096 and 513/512)

Notations

Sagittal

From the appendix to The Sagittal Songbook by Jacob A. Barton, a diagram of how to notate 72edo in the Revo flavor of Sagittal:

JI approximation

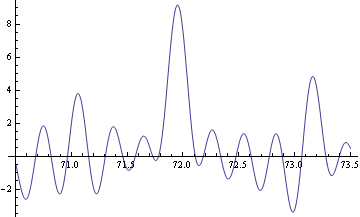
Z function

72edo is the ninth zeta integral edo, as well as being a peak and gap edo, and the maximum value of the Z function in the region near 72 occurs at 71.9506, giving an octave of 1200.824 cents, the stretched octaves of the zeta tuning. Below is a plot of Z in the region around 72.

15-odd-limit interval mappings

The following table shows how 15-odd-limit intervals are represented in 72edo. Prime harmonics are in bold. As 72edo is consistent in the 15-odd-limit, the results by direct approximation and patent val mapping are the same.

15-odd-limit intervals by patent val mapping
Interval, complement	Error (abs, ¢)	Error (rel, %)
1/1, 2/1	0.000	0.0
7/6, 12/7	0.204	1.2
11/6, 12/11	0.637	3.8
7/5, 10/7	0.821	4.9
11/7, 14/11	0.841	5.0
9/5, 10/9	0.930	5.6
5/3, 6/5	1.025	6.2
11/8, 16/11	1.318	7.9
11/10, 20/11	1.662	10.0
9/7, 14/9	1.751	10.5
3/2, 4/3	1.955	11.7
7/4, 8/7	2.159	13.0
15/13, 26/15	2.259	13.6
11/9, 18/11	2.592	15.6
15/14, 28/15	2.776	16.7
5/4, 8/5	2.980	17.9
13/9, 18/13	3.284	19.7
15/11, 22/15	3.617	21.7
9/8, 16/9	3.910	23.5
13/10, 20/13	4.214	25.3
15/8, 16/15	4.935	29.6
13/7, 14/13	5.035	30.2
13/12, 24/13	5.239	31.4
13/11, 22/13	5.876	35.3
13/8, 16/13	7.194	43.2

Regular temperament properties

Subgroup	Comma List	Mapping	Optimal 8ve Stretch (¢)	Tuning Error
Subgroup	Comma List	Mapping	Optimal 8ve Stretch (¢)	Absolute (¢)	Relative (%)
2.3.5	15625/15552, 531441/524288	[⟨72 114 167]]	+0.839	0.594	3.56
2.3.5.7	225/224, 1029/1024, 4375/4374	[⟨72 114 167 202]]	+0.822	0.515	3.09
2.3.5.7.11	225/224, 243/242, 385/384, 4000/3993	[⟨72 114 167 202 249]]	+0.734	0.493	2.96
2.3.5.7.11.13	169/168, 225/224, 243/242, 325/324, 385/384	[⟨72 114 167 202 249 266]]	+0.936	0.638	3.82
2.3.5.7.11.13.17	169/168, 221/220, 225/224, 243/242, 273/272, 325/324	[⟨72 114 167 202 249 266 294]]	+0.975	0.599	3.59

72et has lower relative errors than any previous equal temperaments in the 7-, 11-, 13-, 17-, and 19-limit. The next equal temperaments doing better in these subgroups are 99, 270, 224, 494, and 217, respectively.

Commas

Commas tempered out by 72edo include…

Prime Limit	Ratio^[1]	Monzo	Cents	Name(s)
3	(12 digits)	[-19 12⟩	23.46	Pythagorean comma
5	15625/15552	[-6 -5 6⟩	8.11	Kleisma
5	(16 digits)	[-25 7 6⟩	31.57	Ampersand
5	(18 digits)	[-13 17 -6⟩	15.35	Graviton
5	(26 digits)	[1 -27 18⟩	0.86	Ennealimma
7	225/224	[-5 2 2 -1⟩	7.71	Marvel comma
7	1029/1024	[-10 1 0 3⟩	8.43	Gamelisma
7	2401/2400	[-5 -1 -2 4⟩	0.72	Breedsma
7	4375/4374	[-1 -7 4 1⟩	0.40	Ragisma
7	16875/16807	[0 3 4 -5⟩	6.99	Mirkwai
7	19683/19600	[-4 9 -2 -2⟩	7.32	Cataharry
7	(12 digits)	[-6 -8 2 5⟩	1.12	Wizma
7	(12 digits)	[-4 6 -6 3⟩	0.33	Landscape comma
11	243/242	[-1 5 0 0 -2⟩	7.14	Rastma
11	385/384	[-7 -1 1 1 1⟩	4.50	Keenanisma
11	441/440	[-3 2 -1 2 -1⟩	3.93	Werckisma
11	540/539	[2 3 1 -2 -1⟩	3.21	Swetisma
11	1375/1372	[-2 0 3 -3 1⟩	3.78	Moctdel
11	3025/3024	[-4 -3 2 -1 2⟩	0.57	Lehmerisma
11	4000/3993	[5 -1 3 0 -3⟩	3.03	Wizardharry
11	6250/6237	[1 -4 5 -1 -1⟩	3.60	Liganellus comma
11	9801/9800	[-3 4 -2 -2 2⟩	0.18	Kalisma
11	(14 digits)	[16 -3 0 0 6⟩	2.04	Nexus comma
13	169/168	[-3 -1 0 -1 0 2⟩	10.27	Buzurgisma
13	325/324	[-2 -4 2 0 0 1⟩	5.34	Marveltwin comma
13	351/350	[-1 3 -2 -1 0 1⟩	4.94	Ratwolfsma
13	364/363	[2 -1 0 1 -2 1⟩	4.76	Gentle comma
13	625/624	[-4 -1 4 0 0 -1⟩	2.77	Tunbarsma
13	676/675	[2 -3 -2 0 0 2⟩	2.56	Island comma
13	729/728	[-3 6 0 -1 0 -1⟩	2.38	Squbema
13	1001/1000	[-3 0 -3 1 1 1⟩	1.73	Sinbadma
13	1575/1573	[2 2 1 -2 -1⟩	2.20	Nicola
13	1716/1715	[2 1 -1 -3 1 1⟩	1.01	Lummic comma
13	2080/2079	[5 -3 1 -1 -1 1⟩	0.83	Ibnsinma
13	6656/6655	[9 0 -1 0 -3 1⟩	0.26012	Jacobin comma

↑ Ratios longer than 10 digits are presented by placeholders with informative hints

Rank-2 temperaments

List of edo-distinct 72et rank two temperaments

72edo provides the optimal patent val for miracle and wizard in the 7-limit, miracle, catakleismic, bikleismic, compton, ennealimnic, ennealiminal, enneaportent, marvolo and catalytic in the 11-limit, and catakleismic, bikleismic, compton, comptone, enneaportent, ennealim, catalytic, marvolo, manna, hendec, lizard, neominor, hours, and semimiracle in the 13-limit.

Periods per 8ve	Generator	Names
1	1\72	Quincy
1	5\72	Marvolo
1	7\72	Miracle / benediction / manna
1	11\72
1	13\72
1	17\72	Neominor
1	19\72	Catakleismic
1	23\72
1	25\72	Sqrtphi
1	29\72
1	31\72	Marvo / zarvo
1	35\72	Cotritone
2	1\72
2	5\72	Harry
2	7\72	Semimiracle
2	11\72	Unidec / hendec
2	13\72	Wizard / lizard / gizzard
2	19\72	Bikleismic
3	1\72
3	5\72	Tritikleismic
3	7\72
3	11\72	Mirkat
4	1\72	Quadritikleismic
4	5\72
4	7\72
6	1\72
6	5\72
8	1\72	Octoid
8	2\72	Octowerck
8	4\72
9	1\72
9	3\72	Ennealimmal / ennealimnic
12	1\72	Compton
18	1\72	Hemiennealimmal
24	1\72	Hours
36	1\72

Scales

Smithgw72a, smithgw72b, smithgw72c, smithgw72d, smithgw72e, smithgw72f, smithgw72g, smithgw72h, smithgw72i, smithgw72j
Blackjack, miracle_8, miracle_10, miracle_12, miracle_12a, miracle_24hi, miracle_24lo
Keenanmarvel, xenakis_chrome, xenakis_diat, xenakis_schrome
Euler(24255) genus in 72 equal
JuneGloom
Harry Partch's 43-tone scale: 1 2 2 2 2 1 1 1 2 2 2 1 2 2 2 1 2 2 1 2 2 2 2 2 1 2 2 1 2 2 2 1 2 2 2 1 1 1 2 2 2 2 1
Magnetosphere, Blackened skies, Lost spirit
5- to 10-tone scales in 72edo

Harmonic scale

Mode 8 of the harmonic series – harmonics 8 through 16, octave repeating – is well-represented in 72edo. Note that all the different step sizes are distinguished, except for 13:12 and 14:13 (conflated to 8\72edo, 133.3 cents) and 15:14 and 16:15 (conflated to 7\72edo, 116.7 cents, the generator for miracle temperament).

Harmonics in "Mode 8":	8		9		10		11		12		13		14		15		16
…as JI Ratio from 1/1:	1/1		9/8		5/4		11/8		3/2		13/8		7/4		15/8		2/1
…in cents:	0		203.9		386.3		551.3		702.0		840.5		968.8		1088.3		1200.0
Nearest degree of 72edo:	0		12		23		33		42		50		58		65		72
…in cents:	0		200.0		383.3		550.0		700.0		833.3		966.7		1083.3		1200.0
Steps as Freq. Ratio:		9:8		10:9		11:10		12:11		13:12		14:13		15:14		16:15
…in cents:		203.9		182.4		165.0		150.6		138.6		128.3		119.4		111.7
Nearest degree of 72edo:		12		11		10		9		8		8		7		7
…in cents:		200.0		183.3		166.7		150.0		133.3		133.3		116.7		116.7