29edo

From Xenharmonic Wiki
Jump to navigation Jump to search
← 28edo29edo30edo →
Prime factorization 29 (prime)
Step size 41.3793¢
Fifth 17\29 (703.448¢)
(semiconvergent)
Semitones (A1:m2) 3:2 (124.1¢ : 82.76¢)
Consistency limit 15
Distinct consistency limit 5

29 equal divisions of the octave (abbreviated 29edo or 29ed2), also called 29-tone equal temperament (29tet) or 29 equal temperament (29et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 29 equal parts of about 41.4 ¢ each. Each step represents a frequency ratio of 21/29, or the 29th root of 2.

Theory

29 is the lowest edo which approximates the 3/2 just fifth more accurately than 12edo: 3/2 = 701.955… cents; 17 degrees of 29edo = 703.448… cents. Since the fifth is slightly sharp, 29edo is a positive temperament – a Parapythagorean instead of a Meantone system.

[File info] [File info]
(Super-)pythagorean diatonic major scale and cadence in 29edo 12edo diatonic major scale and cadence, for comparison

The 3 is the only harmonic, of the intelligibly low ones anyway, that 29edo approximates very closely, and it does so quite well. Nonetheless, and rather surprisingly, 29 is the smallest equal division which consistently represents the 15-odd-limit. It is able to do this since it has an accurate 3, and the 5, 7, 11 and 13, while not very accurate, are all tuned flatly. Hence it tempers out a succession of fairly large commas: 250/243 in the 5-limit, 49/48 in the 7-limit, 55/54 in the 11-limit, and 65/64 in the 13-limit. If using these approximations is desired, 29edo actually shines, and it can be used for such things as an alternative to 19edo for negri, as well as an alternative to 22edo or 15edo for porcupine. 29edo is also an oneirotonic tuning with generator 11\29, which generates ammonite temperament.

Another possible use for 29edo is as an equally tempered para-pythagorean scale. Using its fifth as a generator leads to a variant of garibaldi temperament which is not very accurate but which has relatively low 13-limit complexity. However, it gives the POL2 generator for edson temperament with essentially perfect accuracy, only 0.034 cents sharp of it.

Edson is a 2.3.7/5.11/5.13/5 subgroup temperament, and 29 it represents the 2.3.11/5.13/5 subgroup to very high accuracy, and the 2.3.7/5.11/5.13/5 to a lesser but still good accuracy, and so can be used with this subgroup, which is liberally supplied with chords such as the 1-11/7-13/7 (7:11:13) chord, the barbados triad 1-13/10-3/2 (10:13:15), the minor barbados triad 1-15/13-3/2, the 1-14/11-3/2 (22:28:33) triad, the 1-13/11-3/2 triad (22:26:33), and the petrmic triad, a 13-limit essentially tempered dyadic chord. 29 tempers out 352/351, 676/675 and 4000/3993 from the 2.3.11/5.13/5 subgroup, and in addition 196/195 and 364/363 from the 2.3.7/5.11/5.13/5 subgroup, so we have various relationships from the tempering, such as the fact that the 1-13/11-3/2 chord and the 1-14/11-3/2 chord are inverses of each other, a major-minor pairing. A larger subgroup containing both of these subgroups is the 3*29 subgroup 2.3.125.175.275.325; on this subgroup 29 tunes the same as 87, and the commas of 29 on this subgroup are the same as the 13-limit commas of 87. Still another subgroup of interest is the 2*29 subgroup 2.3.25.35.55.65.85; on this subgroup 29 tunes the same as 58 and has the same 17-limit commas.

29edo could be thought of as 12edo's "twin", since the 5-limit error for both is almost exactly the same, but in the opposite direction. There are other ways in which they are counterparts (12 tempers out 50:49 but not 49:48; 29 does the opposite). Each supports a particularly good tonal framework (meantone[7] and nautilus[14], respectively).

A more coincidental similarity is that just as the 12-tone scale is also a 1/2-tone scale (the whole tone being divided into 2 semitones), the 29-tone temperament may also be called 2/9-tone. This is because it has two different sizes of whole tone (4 and 5 steps wide, respectively). So the step size of 29edo may be called a 2/9-tone, just as 24edo's step size is called a quarter tone.

Prime harmonics

Approximation of prime harmonics in 29edo
Harmonic 2 3 5 7 11 13 17 19 23 29 31
Error absolute (¢) +0.0 +1.5 -13.9 -17.1 -13.4 -12.9 +19.2 -7.9 -7.6 +4.9 +13.6
relative (%) +0 +4 -34 -41 -32 -31 +46 -19 -18 +12 +33
Steps
(reduced) 		29
(0) 		46
(17) 		67
(9) 		81
(23) 		100
(13) 		107
(20) 		119
(3) 		123
(7) 		131
(15) 		141
(25) 		144
(28)

Divisors

29edo is the 10th prime edo, following 23edo and coming before 31edo.

Intervals

See also: 29edo solfege
Degree Cents Approx. Ratios of the 13-limit Ups and Downs Notation SKULO interval names and notation (K or S = 1)
0 0.000 1/1 P1 unison D P1 unison D
1 41.379 25/24, 33/32, 56/55, 81/80 ^1, vm2 up unison,
downminor 2nd 		^D, vEb S1, sm2 comma-wide unison, super unison, subminor 2nd KD, SD, sEb
2 82.759 21/20 m2 minor 2nd Eb m2 minor 2nd Eb
3 124.138 16/15, 15/14, 14/13, 13/12 ^m2 upminor 2nd ^Eb Km2 classic minor 2nd KEb
4 165.517 12/11, 11/10, 10/9 vM2 downmajor 2nd vE kM2 comma-narrow/classic major 2nd kE
5 206.897 9/8 M2 major 2nd E M2 major 2nd E
6 248.276 8/7, 7/6, 15/13 ^M2, vm3 upmajor 2nd,
downminor 3rd 		^E, vF SM2, sm3 supermajor 2nd, subminor 3rd SE, sF
·7 289.655 13/11 m3 minor 3rd F m3 minor 3rd F
8 331.034 6/5, 11/9 ^m3 upminor 3rd ^F Km3 classic minor 3rd KF
9 372.414 5/4, 16/13 vM3 downmajor 3rd vF# kM3 classic major 3rd kF#
10 413.793 14/11 M3 major 3rd F# M3 major 3rd F#
11 455.172 9/7, 13/10 ^M3, v4 upmajor 3rd
down 4th 		^F#, vG SM3, s4 supermajor 3rd, sub 4th SF#, sG
·12 496.552 4/3 P4 4th G P4 perfect 4th G
13 537.931 11/8, 15/11 ^4 up 4th ^G K4 comma-wide 4th KG
14 579.310 7/5, 18/13 vA4, d5 downaug 4th,
dim 5th 		vG#, Ab kA4, d5 comma-narrow aug 4th, dim 5th kG#, Ab
15 620.690 10/7, 13/9 A4, ^d5 aug 4th,
updim 5th 		G#, ^Ab A4, Kd5 aug 4th, comma-wide dim 5th G#, KAb
16 662.069 16/11, 22/15 v5 down 5th vA k5 comm-narrow 5th kA
·17 703.448 3/2 P5 5th A P5 perfect 5th A
18 744.828 14/9, 20/13 ^5, vm6 up 5th,
downminor 6th 		^A, vBb S5, sm6 super 5th, subminor 6th SA, sBb
19 786.207 11/7 m6 minor 6th Bb m6 minor 6th Bb
20 827.586 8/5, 13/8 ^m6 upminor 6th ^Bb Km6 classic minor 6th KBb
21 868.966 5/3, 18/11 vM6 downmajor 6th vB kM6 classic major 6th kB
·22 910.345 22/13 M6 major 6th B M6 major 6th B
23 951.724 7/4, 12/7, 26/15 ^M6, vm7 upmajor 6th,
downminor 7th 		^B, vC SM6, sm7 supermajor 6th, subminor 7th SB, sC
24 993.103 16/9 m7 minor 7th C m7 minor 7th C
25 1034.483 11/6, 20/11, 9/5 ^m7 upminor 7th ^C Km7 comma-wide/classic minor 7th KC
26 1075.862 15/8, 28/15, 13/7, 24/13 vM7 downmajor 7th vC# kM7 classic major 7th kC#
27 1117.241 40/21 M7 major 7th C# M7 major 7th C#
28 1158.621 48/25, 64/33, 55/28, 160/81 ^M7, v8 upmajor 7th,
down 8ve 		^C#, vD SM7, s8 supermajor 7th, comma-narrow 8ve, sub 8ve SC#, kD, sD
29 1200.000 2/1 P8 8ve D P8 8ve D

Combining ups and downs notation with color notation, qualities can be loosely associated with colors:

quality color name monzo format examples
downminor zo {a, b, 0, 1} 7/6, 7/4
minor fourthward wa {a, b}, b < -1 32/27, 16/9
upminor gu {a, b, -1} 6/5, 9/5
" ilo {a, b, 0, 0, 1} 11/9, 11/6
downmajor lu {a, b, 0, 0, -1} 12/11, 18/11
" yo {a, b, 1} 5/4, 5/3
major fifthward wa {a, b}, b > 1 9/8, 27/16
upmajor ru {a, b, 0, -1} 9/7, 12/7

All 29edo chords can be named using ups and downs. Alterations are always enclosed in parentheses, additions never are. An up or down immediately after the chord root affects the 3rd, 6th, 7th, and/or the 11th (every other note of a stacked-3rds chord 6-1-3-5-7-9-11-13). Here are the zo, gu, yo and ru triads:

color of the 3rd JI chord notes as edosteps notes of C chord written name spoken name
zo 6:7:9 0-6-17 C vEb G Cvm C downminor
gu 10:12:15 0-8-17 C ^Eb G C^m C upminor
yo 4:5:6 0-9-17 C vE G Cv C downmajor or C down
ru 14:18:21 0-11-17 C ^E G C^ C upmajor or C up

For a more complete list, see Ups and Downs Notation #Chords and Chord Progressions.

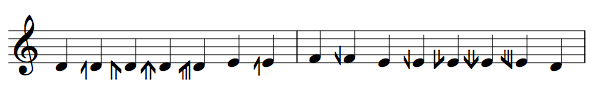
29edothumb.png
this example in Sagittal notation shows 29-edo as a fifth-tone system.

Approximation to JI

15-odd-limit interval mappings

The following table shows how 15-odd-limit intervals are represented in 29edo. Prime harmonics are in bold. As 29edo is consistent in the 15-odd-limit, the results by direct approximation and patent val mapping are identical.

15-odd-limit intervals by patent val mapping
Interval, complement Error (abs, ¢) Error (rel, %)
1/1, 2/1 0.000 0.0
13/11, 22/13 0.445 1.1
11/10, 20/11 0.513 1.2
15/13, 26/15 0.535 1.3
13/10, 20/13 0.958 2.3
15/11, 22/15 0.980 2.4
3/2, 4/3 1.493 3.6
9/8, 16/9 2.987 7.2
7/5, 10/7 3.202 7.7
11/7, 14/11 3.715 9.0
13/7, 14/13 4.160 10.1
15/14, 28/15 4.695 11.3
15/8, 16/15 12.407 30.0
13/8, 16/13 12.941 31.3
11/8, 16/11 13.387 32.4
5/4, 8/5 13.900 33.6
13/12, 24/13 14.435 34.9
11/6, 12/11 14.880 36.0
5/3, 6/5 15.393 37.2
13/9, 18/13 15.928 38.5
11/9, 18/11 16.373 39.6
9/5, 10/9 16.886 40.8
7/4, 8/7 17.102 41.3
7/6, 12/7 18.595 44.9
9/7, 14/9 20.088 48.5

Regular temperament properties

Subgroup Comma list Mapping Optimal
8ve Stretch (¢) 		Tuning Error
Absolute (¢) Relative (%)
2.3 [46 -29⟩ [⟨29 46]] -0.47 0.47 1.14
2.3.5 250/243, 16875/16384 [⟨29 46 67]] +1.68 3.07 7.41
2.3.5.7 49/48, 225/224, 250/243 [⟨29 46 67 81]] +2.78 3.28 7.91
2.3.5.7.11 49/48, 55/54, 100/99, 225/224 [⟨29 46 67 81 100]] +3.00 2.97 7.15
2.3.5.7.11.13 49/48, 55/54, 100/99, 105/104, 225/224 [⟨29 46 67 81 100 107]] +3.09 2.71 6.54
2.3.5.7.11.13.19 49/48, 55/54, 65/64, 77/76, 100/99, 105/104 [⟨29 46 67 81 100 107 123]] +2.91 2.55 6.16
2.3.5.7.11.13.19.23 49/48, 55/54, 65/64, 70/69, 77/76, 100/99, 105/104 [⟨29 46 67 81 100 107 123 131]] +2.76 2.42 5.85

29et (29g val) has a lower relative error than any previous equal temperament in the 23-limit. The next equal temperament doing better in this subgroup is 46.

29et does well in the no-17 19-limit and no-17 23-limit, being consistent to the no-17 23-odd-limit. However, 15edo is lower in relative error in both these subgroups than 29.

Commas

29edo tempers out the following commas. This assumes the patent val ⟨29 46 67 81 100 107]. Cent values are rounded to 5 digits.

Prime
Limit 		Ratio[1] Monzo Cents Color name Name(s)
3 (28 digits) [46 -29⟩ 43.305 Wa-29 29-comma, mystery comma
5 16875/16384 [-14 3 4⟩ 51.120 Laquadyo Negri comma, double augmentation diesis
5 250/243 [1 -5 3⟩ 49.166 Triyo Porcupine comma, maximal diesis
5 32805/32768 [-15 8 1⟩ 1.9537 Layo Schisma
7 525/512 [-9 1 2 1⟩ 43.408 Lazoyoyo Avicennma, Avicenna's enharmonic diesis
7 49/48 [-4 -1 0 2⟩ 35.697 Zozo Slendro diesis
7 686/675 [1 -3 -2 3⟩ 27.985 Trizo-agugu Senga
7 64827/64000 [-9 3 -3 4⟩ 22.227 Laquadzo-atrigu Squalentine
7 3125/3087 [0 -2 5 -3⟩ 21.181 Triru-aquinyo Gariboh
7 50421/50000 [-4 1 -5 5⟩ 14.516 Quinzogu Trimyna
7 4000/3969 [5 -4 3 -2⟩ 13.469 Rurutriyo Octagar
7 225/224 [-5 2 2 -1⟩ 7.7115 Ruyoyo Septimal kleisma, marvel comma
7 5120/5103 [10 -6 1 -1⟩ 5.7578 Saruyo Hemifamity
7 (16 digits) [25 -14 0 -1⟩ 3.8041 Sasaru Garischisma
11 100/99 [2 -2 2 0 -1⟩ 17.399 Luyoyo Ptolemisma
11 121/120 [-3 -1 -1 0 2⟩ 14.367 Lologu Biyatisma
11 896/891 [7 -4 0 1 -1⟩ 9.6880 Saluzo Pentacircle
11 441/440 [-3 2 -1 2 -1⟩ 3.9302 Luzozogu Werckisma
11 4000/3993 [5 -1 3 0 -3⟩ 3.0323 Trithuyo Wizardharry
13 91/90 [-1 -2 -1 1 0 1⟩ 19.130 Thozogu Superleap
  1. ↑ Ratios longer than 10 digits are presented by placeholders with informative hints

Rank-2 temperaments

Table of rank-2 temperaments by generator
Periods
per 8ve 		Generator
(Reduced) 		Cents
(Reduced) 		Associated Ratio
(Reduced) 		Temperament
1 2\29 82.8 21/20 Nautilus
1 3\29 124.1 14/13 Negri / negril / negroni
1 4\29 165.5 11/10 Porky / coendou
1 5\29 206.9 9/8 Baldy
1 6\29 248.3 15/13 Immunity / immune
Hemigari
1 7\29 289.7 13/11 Gariberttet
1 8\29 331.034 23/19 Rarity
1 9\29 372.4 5/4 Sephiroth
1 10\29 413.8 9/7 Roman
1 11\29 455.2 13/10 Ammonite
1 12\29 496.6 4/3 Garibaldi / andromeda
Leapday
1 13\29 537.9 15/11 Wilsec
1 14\29 579.3 7/5 Tritonic
1 17\29 703.4 3/2 Edson

Important MOSes include:

The Tetradecatonic System

A variant of porcupine supported in 29edo is nautilus, which splits the porcupine generator in half (tempering out 49:48 in the process), thus resulting in a different mapping for 7 than standard porcupine. Nautilus also extends to the 13-limit much more easily than does standard porcupine.

The MOS nautilus[14] contains both "even" tetrads (approximating 4:5:6:7 or its inverse) as well as "odd" tetrads (approximating the "Bohlen-Pierce-like" chord 9:11:13:15, or its inverse). Both types are recognizable and consonant, if somewhat heavily tempered. Moreover, one of the four types of tetrads may be built on each scale degree of nautilus[14], thus there are as many chords as there are notes, so nautilus[14] has a "circulating" quality to it with as much freedom of modulation as possible. To be exact, there are 4 "major-even", 4 "minor-even", 3 "major-odd", and 3 "minor-odd" chords.

Nautilus[14] scale (Lsssssssssssss) in 29edo

Fourteen-note MOSes are worth looking at because taking every other note of them gives a heptatonic, and in many cases diatonic-like, scale. Nautilus[14] is no exception; although the resulting porcupine "diatonic" scale sounds somewhat different from diatonic scales generated from fifths, it can still provide some degree of familiarity. Furthermore, every diatonic chord progression will have at least one loose analogue in nautilus[14], although the chord types might change (for instance, it is possible to have a I-IV-V chord progression where the I is major-odd, and the IV and V are both major-even; the V in this case being on a narrow or "odd" fifth rather than a perfect or "even" fifth).

The fact that the generator size is also a step size means that nautilus makes a good candidate for a generalized keyboard; the fingering of nautilus[14] becomes very simple as a result, perhaps even simpler than with traditional keyboards, despite there being more notes.

If one can tolerate the tuning error (which is roughly equal to that of 12edo, albeit in the opposite direction for the 5- and 7-limits), this tetradecatonic scale is worth exploring. 29edo is often neglected since it falls so close to the much more popular and well-studied 31edo, but 29 does have its own advantages, and this is one of them.

Nicetone

29edo is not a meantone system, but it could nonetheless be used as a basis for common-practice music if one considers the superfourth as a consonant, alternative type of fourth, and the 11:13:16 as an alternative type of consonant "doubly minor" triad. We can then use a diatonic scale such as 5435453 (which resembles Didymus' 5-limit JI diatonic scale, but with the syntonic comma being exaggerated in size). This scale has a very similar harmonic structure to a meantone diatonic scale, except that one of its minor triads is doubly-minor.

Such a scale could be called "nicetone" as a play on meantone. Since it preserves most of the same 5-limit relationships, nicetone is only slightly xenharmonic (in contrast to superpyth, which is quite blatantly so). The fact that 29edo's superfourth is within a cent of 15:11, and its 13:11 is within half a cent of a just 13:11, are both happy accidents. One just has to make sure that one is using a timbre that allows these higher-limit harmonic relationships to sound apparent and consonant enough to substitute for their simpler counterparts. The nicetone scale is also the cradle of the superdiatonic scales 522352253 and 3243324323 in between the leapfrog diatonic and chromatic scales.

Nicetone scale 5435453 and cadence in 29edo

Scales

MOS scales

Main article: 29edo/MOS scales

Well temperaments

Instruments

Guitar 29EDO from Peru - Charles Loli and Antonio Huamani

Loli-huamani-29edo-guitar-f 735065b21747.jpg

Bass 29EDO from Peru - Charles Loli and Antonio Huamani

External image: https://fbcdn-sphotos-c-a.akamaihd.net/hphotos-ak-prn1/r90/550502_538613626155939_2005925977_n.jpg

WARNING: MediaWiki doesn't have very good support for external images.
Furthermore, since external images can break, we recommend that you replace the above with a local copy of the image.

Music

Modern renderings

Johann Sebastian Bach
Nicolaus Bruhns

21st century

Charles Loli A. (site[dead link])
Bryan Deister
E8 Heterotic
Francium
Igliashon Jones
Budjarn Lambeth
NullPointerException Music
Mats Öljare
Ray Perlner
Chris Vaisvil
Xotla

See also

Retrieved from "https://en.xen.wiki/index.php?title=29edo&oldid=140011"